Kongruenzsätze: Dreiecke konstruieren
12 Mathe-Arbeitsblätter mit Lösungen
Kongruenz bedeutet: Zwei Figuren, die gleiche Seitenlängen und Winkelgrößen haben, sind immer deckungsgleich. Mit anderen Worten: Zwei Dreiecke, die ich durch Verschieben, Drehen und Spiegeln genau übereinander legen kann, sind kongruent zueinander.
Mit Hilfe der Kongruenzsätze SSS, SWS, SSW und WSW kannst Du aus gegebenen Werten Dreiecke konstruieren. Egal wie Du das Blatt hälst oder mit welcher Seite Du beginnst, es kommen immer die gleichen Dreiecke heraus.
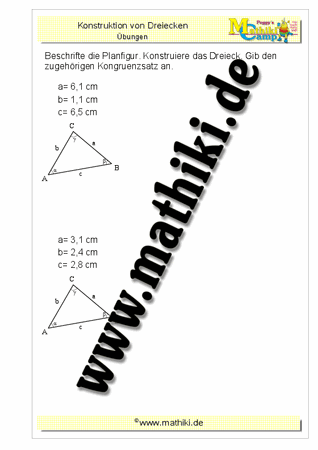
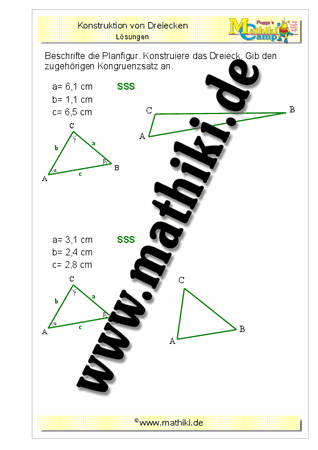
SSS bedeutet: Wenn drei Seiten in einem Dreieck gegeben sind, kann das Dreieck konstruiert werden. Wichtig dabei ist, dass die Summe der beiden kürzeren Seiten immer größer als die längste Seite im Dreieck sein muss. Ansonsten kann das Dreieck nicht konstruiert werden, da sich die beiden kürzeren Seiten niemals berühren würden.
SWS bedeutet: Wenn zwei Seiten und der eingeschlossene Winkel gegeben sind, kann ein Dreieck konstruiert werden.
WSW bedeutet: Wenn eine Seite und die beiden anliegenden Winkel gegeben sind, kann das Dreieck auch konstruiert werden. Wichtig dabei ist, dass die Summe der beiden Winkel kleiner als 180° sein muss. Da die Winkelsumme in einem Dreieck 180° beträgt, muss die Summe von zwei Winkeln immer kleiner als 180° sein. Sind die beiden Winkel schon größer oder gleich 180°, dann bleibt für den dritten Winkel nichts mehr übrig.
SSW bedeutet: Wenn zwei Seiten und der Winkel gegenüber der längeren Seite gegeben sind, kann das Dreieck auch konstruiert werden.
Für die Konstruktion der einzelnen Dreiecke benötigst Du ein Geodreieck, einen Zirkel und einen feinen Bleistift. Versuche möglichst dünne Linien zu ziehen. Erst wenn Du alles korrekt gezeichnet hast, kannst Du die Linien des entstandenen Dreiecks noch einmal ein wenig nachziehen.
Das erste Arbeitsblatt vom Thema "Kongruenzsätze: Dreiecke konstruieren" kannst Du kostenlos herunterladen.

Kongruenzsätze: Mit SSS Dreiecke konstruieren
Gegeben sind immer drei Seiten eines Dreiecks. Konstruiere mit Geodreieck und Zirkel das gesuchte Dreieck.
![]() Arbeitsblatt 2 + Lösung - (mit Kunden-Login)
Arbeitsblatt 2 + Lösung - (mit Kunden-Login)
![]() Arbeitsblatt 3 + Lösung - (mit Kunden-Login)
Arbeitsblatt 3 + Lösung - (mit Kunden-Login)
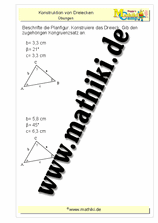
Kongruenzsatz SSW
Gegeben sind immer zwei Seiten und ein Winkel eines Dreiecks. Konstruiere mit Geodreieck und Zirkel das gesuchte Dreieck.
![]() Arbeitsblatt 1 + Lösung - (mit Kunden-Login)
Arbeitsblatt 1 + Lösung - (mit Kunden-Login)
![]() Arbeitsblatt 2 + Lösung - (mit Kunden-Login)
Arbeitsblatt 2 + Lösung - (mit Kunden-Login)
![]() Arbeitsblatt 3 + Lösung - (mit Kunden-Login)
Arbeitsblatt 3 + Lösung - (mit Kunden-Login)
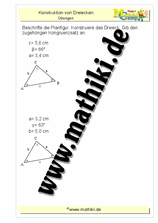
Kongruenzsatz SWS
Gegeben sind immer zwei Seiten und der eingeschlossene Winkel eines Dreiecks. Konstruiere mit Geodreieck und Zirkel das gesuchte Dreieck.
![]() Arbeitsblatt 1 + Lösung - (mit Kunden-Login)
Arbeitsblatt 1 + Lösung - (mit Kunden-Login)
![]() Arbeitsblatt 2 + Lösung - (mit Kunden-Login)
Arbeitsblatt 2 + Lösung - (mit Kunden-Login)
![]() Arbeitsblatt 3 + Lösung - (mit Kunden-Login)
Arbeitsblatt 3 + Lösung - (mit Kunden-Login)
Kongruenzsätze: Mit WSW Dreiecke konstruieren
Gegeben sind immer eine Seite und die daran angrenzenden Winkel eines Dreiecks. Konstruiere mit Geodreieck und Zirkel das gesuchte Dreieck.
![]() Arbeitsblatt 1 + Lösung - (mit Kunden-Login)
Arbeitsblatt 1 + Lösung - (mit Kunden-Login)
![]() Arbeitsblatt 2 + Lösung - (mit Kunden-Login)
Arbeitsblatt 2 + Lösung - (mit Kunden-Login)
![]() Arbeitsblatt 3 + Lösung - (mit Kunden-Login)
Arbeitsblatt 3 + Lösung - (mit Kunden-Login)
[Zurück]